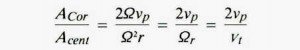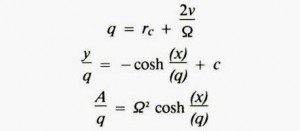SSI UPDATE
THE HIGH FRONTIER® NEWSLETTER
VOLUME XX ISSUE 2 MARCH/APRIL 1994
SPACE STUDIES INSTITUTE
P.O. BOX 82
PRINCETON, NEW JERSEY 08542
[[librarian note: This address is here, as it was in the original printed newsletter, for historical reasons. It is no longer the physical address of SSI. For contributions, please see this page]]
DIRECTOR’S COLUMN
A is for Asteroid
B is for Batcave
C is for Clementine …
A few blocks away from the Washington Metro Line in Alexandria, Virginia is a nondescript warehouse in a run-down neighborhood. It looks precisely like the urban lair of every Marvel comic book villain – right down to the roll-up corrugated metal garage door. Just as in the comics, a fantastic secret lies behind these walls. This warehouse is actually the control center for Clementine, the low-cost lunar and asteroid mission. Mindful of the unusual nature of their headquarters, the mission operators have dubbed it “The Batcave.”
At this small command center, the images from Clementine’s lunar polar orbit mapping are being recorded. Preparations are also underway for the next phase of Clementine’s mission – a close fly-by of the asteroid Geographos.
Edward O’Neill and I visited the Batcave in early March prior to a national press conference on the Clementine mission at the Pentagon. At this briefing, Colonel Pedro Rustan, the Mission Manager for the Clementine project, dedicated the mission to SSI’s founder, Dr. Gerard K. O’Neill. Rustan presented a commemorative plaque to Edward and recounted Gerry’s pioneering work on space resources and his interest in small space prospecting missions to the Moon and the asteroids.
Dr. Stuart Nozette, Deputy Mission Manager for Clementine told us that reading O’Neill’s 1974 Physics Today article, “The Colonization of Space,” had a profound impact on his life. “Before learning about space resources, I was planning to go to medical school,” he recounted. “Gerry’s article gave me a new direction.”
Two Asteroids for the Price of One?
Clementine is currently scheduled to blast out of lunar orbit in early May to prepare for its encounter with Geographos, a near-Earth asteroid named in honor of the National Geographic Society. Thanks to the very precise performance of the Morton Thiokol Star solid motor in the upper stage, Clementine was able to minimize corrective burns on its way to the Moon. As a result, there is a bit of surplus delta-vee in the tanks. (About 150 meters per second capability over budget.) Consequently there is a good chance that the mission could undertake a fly-by of a second asteroid following the Geographos encounter. Asteroid 1983RD is under discussion as a candidate for such a second fly-by.
Gregg Maryniak
DESIGNING FOR LIFE AND MOTION IN ARTIFICIAL-GRAVITY ENVIRONMENTS
By Theodore W. Hall
Architecture and Planning Research Laboratory
University of Michigan, Ann Arbor, Michigan
Ted successfully defended his doctoral dissertation in architecture on February 9, 1994. “The Architecture of Artificial-Gravity Environments for Long-Duration Space Habitation” will be published through University Microfilms Inc.
Abstract
Artists’ conceptions of artificial-gravity environments are often misleading because they fail to express the dynamics of relative motion in a rotating reference. Exploring these dynamics through mathematical derivation and computer simulation can lead to more empathic representations of certain peculiar aspects of life and motion in artificial gravity. The goal of environmental design in artificial gravity is not to fool people into thinking they’re on Earth, but rather, to help them orient themselves to the realities of their rotating environment. (This article is distilled from Dr. Hall’s SSI conference papers of 1991 and 1993 and Chapter 4 of his dissertation.)
Introduction
Artificial gravity is often presented as a panacea for all of the ills associated with prolonged weightlessness. While extensive study has been devoted to the design of the artifact (structure, stability, propulsion, and so on), relatively little has been written about the design of the environment, from the point of view of an inhabitant living and moving within it. It has often been implied, and sometimes stated outright, that artificial gravity should permit the adoption of essentially terrestrial designs; the artificiality of the gravity has been downplayed. But saccharin is not sucrose, and centripetal acceleration is not gravity as we know it.
This article examines the relationship between the physics of rotation and the perception of comfort from the point of view of a person living and moving within a rotating environment. For the purposes of this article, I will omit the proofs and focus on a few of the more tangible results. For a fuller treatment, see the 1991 and 1993 SSI conference proceedings.
Components of Artificial Gravity
Acceleration by any force other than gravity produces a sensation of weight. Gravity acting alone produces a sensation of weightlessness. Earth weight results not from the downward pull of gravity, but from the equal and opposite upward push of the ground.
When people or objects move within a rotating environment, they undergo acceleration in inertial space that may be neither intended nor expected. These extra accelerations distort the apparent gravity. The total acceleration in inertial space is:
(Boldface symbols represent vectors; italics indicate scalar magnitudes; dots above indicate derivatives with respect to time.)
Only the first term![]() represents “design gravity.” The others represent gravitational distortions that result from motion within the environment. The goal is to design the environment such that the first term alone yields some preferred acceleration while simultaneously minimizing the others. Equation 1 suggests three strategies:
represents “design gravity.” The others represent gravitational distortions that result from motion within the environment. The goal is to design the environment such that the first term alone yields some preferred acceleration while simultaneously minimizing the others. Equation 1 suggests three strategies:
• Restrict the direction of local motion to be parallel to the axis of rotation. In this case the second and third terms of equation 1 vanish. Unfortunately, eccentric motion parallel to the axis tends to destabilize the rotation – causing the axis to wobble and invalidating the initial assumption of constant angular velocity.
• Minimize the speed of local motion. This seems to imply some type of behavior modification, whether through individual experience and aversion to motion sickness, deliberate training, or mechanical restraint.
• Minimize the angular velocity of the environment. This requires maximizing the radius, as dictated by the first term of equation 1. The net effect is to minimize the other terms.
One measure of gravitational distortion is the ratio of the magnitudes of Coriolis and centripetal accelerations. Define the following
symbols:
ACor is the magnitude of the Coriolis acceleration:
Acent is the magnitude of the centripetal acceleration:
vp is the magnitude of relative velocity perpendicular to the environment’s axis of rotation.
Vt is the magnitude of the environment’s tangential velocity (rim speed) in inertial space.
If decreasing angular velocity is compensated by increasing radius, so that centripetal acceleration remains constant, then decreasing angular velocity Ω decreases this ratio:
However, once the maximum feasible radius is reached, further reduction of angular velocity Ω decreases both the Coriolis and centripetal accelerations, and increases the ratio of Coriolis to centripetal:
Thus for any given radius, while reducing Ω ameliorates problems associated with rotational cross-coupling (such as dizziness, ataxia, and nausea), it exacerbates gravitational distortion.
Comfort
Based on experiments in centrifuges and slow rotation rooms, researchers have developed various comfort charts for artificial gravity [1-6]. These charts specify boundary values for rotational parameters in an attempt to limit the adverse effects of Coriolis accelerations and cross-coupled rotations. They are succinct summaries of abstract mathematical relationships, but they do nothing to convey the look and feel of artificial gravity. Consequently, there has been a tendency in many design concepts to treat any point within the comfort zone as “essentially terrestrial,” although that has not been the criterion for defining the zone. The defining criterion has been “mitigation of symptoms,” and authors differ as to the boundary values that satisfy it. This suggests that the comfort boundaries are fuzzier than the individual charts imply, and that comfort may be influenced by task requirements and environmental design considerations beyond the basic rotational parameters.
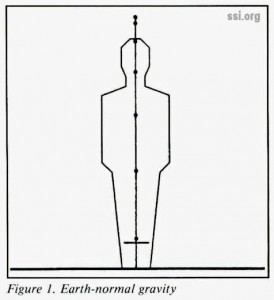
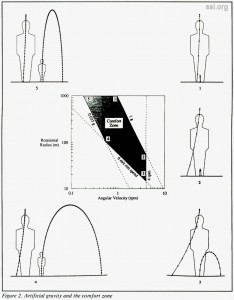
Perhaps a more intuitive way to compare artificial-gravity environments with each other as well as with Earth is to observe the behavior of a free-falling object when dropped from a certain height or launched from the floor with a certain velocity. Such a comparison is suggested in figures 1 and 2. Figure 1 shows for Earth-normal gravity the effect of hopping vertically off the floor with an initial velocity of 2 meters per second and of dropping a ball from an initial height of 2 meters. The “hop” and the “drop” each trace vertical trajectories; the “hop” reaches a maximum height of 0.204 meters (8.03 inches), indicated by a short horizontal line; the “drop” is marked by dots at 0.1-second intervals. Figure 2 shows a typical comfort chart for artificial gravity, after that of Hill and Schnitzer [1], surrounded by five similar “hop and drop” diagrams one for each boundary point of the comfort zone. When compared with the Earth-normal “yardstick” of figure 1, these diagrams reveal certain features of the comfort boundaries:
• Large radius – points 5 and 1: Artificial gravity becomes increasingly “normal” as the radius of rotation approaches infinity. The trajectory of a dropped objects depends only on the radius of rotation and the initial height of the object. Thus, the drops at points 5 and 1 follow congruent paths, although the drop at 5 is much slower due to the low gravity. (The dots are spaced at 0.1-second intervals.) The trajectory of a thrown object is influenced by the ratio of its initial relative velocity to the tangential velocity (rim speed) of the environment. Thus the hop at point 5, besides being much higher (due to the low gravity), is also more distorted than at point 1 due to the lower tangential velocity. Point 1 is the most “Earth-normal” point on the chart; point 5 approaches “normal” for a planetesimal or asteroid.
• Earth gravity – points 1 and 2: Earth-magnitude does not imply Earth-normal. Although both points represent 1-g environments, both the hop and the drop are more distorted at point 2, due to the smaller radius and lower tangential velocity.
• High angular velocity – points 2 and 3: The upper limit of angular velocity is determined by the onset of motion sickness due to cross-coupled rotations. At this boundary, reducing the radius reduces the centripetal acceleration and tangential velocity as well. As judged by the “twisting” of the apparent gravitational field, point 3 is the least normal point in the comfort zone.
• Low tangential velocity – points 3 and 4: For a given relative motion, the ratio of Coriolis to centripetal acceleration increases as tangential velocity decreases. Between points 3 and 4 it is constant, and the hops at these points have similar shapes, though the hop at point 4 is larger due to the lower acceleration. The drop at point 4 is straighter due to the larger radius.
• Low gravity – points 4 and 5: Although the centripetal acceleration at these points is equal, the gravitational environment is less distorted at point 5 due to its larger radius and higher tangential velocity.
Evidently, the comfort zone encompasses a wide range of environments many of them substantially non-terrestrial. Conformance to the comfort zone does not guarantee an Earthnormal gravity environment, nor does it sanction “essentially terrestrial” design.
Linear Motion and Catenary Slope
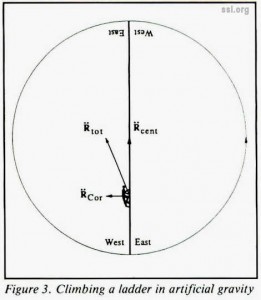
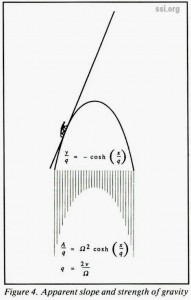
For linear motion at constant speed in a rotating environment, the perceived gravity varies in both magnitude and direction. Figures 3 and 4 show one example of this type of motion: climbing a ladder. Figure 3 shows the acceleration of the climber from an inertial reference. Figure 4 shows the apparent slope of the ladder from the climber’s gravitational reference. The apparent slope follows a catenary curve:
where:
rc is the rotational radius to the midpoint of the chord.
v is the constant speed relative to the chord.
Ω is the rotational speed of the environment (radians per unit time).
A is the magnitude of the apparent gravity.
c is an arbitrary constant of integration.
(In the example of figures 3 and 4, the chord of the ladder passes through the center of rotation, and rc is zero.)
Ladders in artificial-gravity environments should be oriented such that the climber is pressed into the curve from above, rather than pulled away from below or sideways. The plane of the ladder should be perpendicular to the plane of rotation. Because the Coriolis acceleration reverses with the direction of travel, the ladder should be accessible from both sides. To stay on top of the curve, the user should ascend on the west (retrograde) side, as shown, and descend on the east (prograde) side.
A similar catenary slope would occur when walking on a flat floor tangent to the rotation – for example, in a straight cylindrical habitat module arranged “horizontally” in a toroidal or tethered system. The effect would be similar to walking on a teeter-totter, but less pronounced when the radius of rotation (rc) is large relative to the length of the module.
In assessing the significance of apparent slope, it is helpful to consider a few guidelines from Earthly design Table 1 has been culled from the BOCA National Building Code [7-8], Templer [9], Hesselgren (10], derivation, and personal observation.
People are generally poor judges of slope, and tend to over-estimate the steepness of hills. An incline of 5° feels much steeper to a pedestrian than it looks on paper. After estimating the apparent slope for relative motion in an artificial-gravity environment, comparison with values such as those in table 1 may indicate whether the architectural paradigm should be terrestrial, or naval, or something else entirely.
| Table 1. Typical Slopes in Terrestrial Architecture | |
|---|---|
| Condition: | Slope |
| Maximum slope for residential stairs (8.25″ riser, 9″ tread) |
42.5° |
| Maximum slope for public stairs (7″ riser, 11″ tread) |
32.5° |
| Maximum slope for means-of-egress ramps for healthy persons (1:8) |
7.1° |
| Maximum slope for means-of-egress ramps for handicapped persons (1:12) |
4.8° |
| Slope at which warning signs are posted on some highways (8% grade) |
4.6° |
| Maximum wash of stair tread (1:60) | 1.0° |
| Slope sufficient for water run-off, but not generally perceived (1:100) |
0.6° |
| End-point rotation of simply-supported, uniformly-loaded floor beam under maximum deflection (deflectionmax = span/360) |
0.5° |
| Minimum slope for 2.5″ sewage drain (1/4 inch per foot) |
1.2° |
| Minimum slope for 8″ sewage drain (1/16 inch per foot) |
.03° |
Adaptive Design
Descriptions of artificial-gravity environments have often stressed how Earth-like they could be. But, O’Neill noted how structural mass increases rapidly with radius as angular velocity decreases toward zero [11], and Stone and Cramer have suggested that acceptable Coriolis forces in material handling may be as high as 25% of the centripetal forces [4-5]. “Earth-normal” artificial gravity will come at a high price. The first artificial-gravity environments – research facilities and interplanetary vehicles – are likely to be far from “normal.” A carefully planned, deliberately nonterrestrial work environment may permit a smaller radius by orienting relative motion so as to minimize gravitational disportion and provide workers with the best mechanical advantage in overcoming it.
There is also a philosophical issue: One should not fly to Hong Kong and expect to find Des Moines. Similarly, there is no reason to expect space colonies to look like San Francisco or Ann Arbor. The High Frontier cannot be successfully settled by people wishing they were back on Earth. It is reasonable to expect – even demand – that the first colonists will be adventurous types looking for new experiences. For their sake, Island One should be designed with a fountain or two – as figure 5 shows – the possibilities are truly out of this world!
References
1. Paul R. Hill and Emanuel Schnitzer. “Rotating Manned Space Stations.” Astronautics, vol. 7, no. 9, p. 4-28, September 1962. American Rocket Society.
2. Robert R. Gilruth. “Manned Space Stations Gateway to our Future in Space.” Manned Laboratories in Space, p. 1-10. Edited by S. Fred Singer. Springer-Verlag, 1969.
3. Theodore J. Gordon and Robert Gervais. “Critical Engineering Problems of Space Stations.” Manned Laboratories in Space, p. 11-32. Edited by S. Fred Singer. Springer-Verlag, 1969.
4. Ralph W . Stone. “An Overview of Artificial Gravity.” Fifth Symposium on the Role of the Vestibular Organs in Space Exploration, p. 23-33 . NASA Scientific and Technical Information Division, 1973. Special Publication 115
5. D. Bryant Cramer. “Physiological Considerations of Artificial Gravity.” Applications of Tethers in Space, vol. I, p. 3·95-3·107. Edited by Alfred C. Cron. NASA Scientific and Technical Information Branch, 1985. Conference Publication 2364.
6. NASA. Man-System Integration Standards. NASASTD-3000, vol. I, sec. 5.3.2.3, March 1987.
7. BOCA. The BOCA National Building Code, 1990, eleventh edition, sections 817.6, 1306.3.2. Building Officials and Code Administrators International, Inc., 1989.
8. BOCA. The BOCA National Plumbing Code, 1990, eighth edition, sections P-602.1, P-803.1. Building Officials and Code Administrators International, Inc., 1989.
9. John Templer. The Staircase: Studies of Hazards, Falls, and Safer Design, page 149. MIT Press, 1992.
10. Sven Hesselgren. The Language of Architecture, page 163. Studentlitteratur, Lund, Sweden, 1969.
11. Gerard K. O’Neill. “Maximum-Strength, Minimum-Mass Structures.” Space-Based Manufacturing from Nonterrestrial Materials, p. 161-
171 . Edited by Gerard K. O’Neill and Brian O’Leary. American Institute of Aeronautics and Astronautics, 1977.
ABOUT THE INSTITUTE
The Space Studies Institute is a nonprofit, international, research and educational organization. Founded in 1977, it is dedicated to opening the high frontier of space.
SSI’s goals include using the material wealth and solar energy of space to improve the human condition both for those who live on Earth and those who live in space, and building Earth-like habitats in space to expand the ecological range of humanity throughout the solar system and ultimately, perhaps, throughout the galaxy.
To this end, SSI has conducted and is conducting pioneering research into advanced space propulsion, the extraction and processing of nonterrestrial materials for engineering purposes, and the identification and location of lunar and asteroidal resources.
Following are four opportunities for participation in SSI activities:
Corporate Membership
SSI’s Corporate Membership program offers access to SSI’s broad base of technical advisors, access to a resume pool, and access to exhibit space at the biennial SSI Conference on Space Manufacturing. Research partnerships are encouraged.
Senior Associate Program
The Senior Associates Program is currently SSI’s largest source of funds for High Frontier® research and education. The program also provides a way for anyone interested in the High Frontier to play a key role in making space colonization and space manufacturing achievable within our lifetimes. Following is a description of the program.
The Senior Associate program was created in 1979 to generate the steady funds that SSI needs to conduct research projects, most of which require money for several years. Today we have about 1,000 active Senior Associates; 537 Senior Associates are on their second, third, or fourth pledge. The program provides about 60% of SSI’s annual budget and is essential to both our research and educational activities.
Senior Associates receive special benefits as our thanks for their support. These benefits include invitations to special events, free mailings of publications by SSI, NASA, and other space organizations; and confidential newsletters, describing SSI developments before they are made public.
However, most people become Senior Associates because they want to see space colonization become a reality; they give much needed funds and join the group of people working to create the High Frontier in our lifetimes. As Senior Associates, they also meet others who share their enthusiasm for space exploration and development. Each Senior Associate makes a five-year pledge to SSI, choosing one of the ranks below:
Associate: $100.00 annually
Fellow: $200.00 annually
Colleague: $300.00 annually
Distinguished Colleague: $500.00 annually
Payments can be made annually, semiannually, quarterly, or monthly.
Each Senior Associate receives a number with his or her rank, indicating when he or she joined the program. For example, the next person to join could become Fellow 368, or Distinguished Colleague 126. Each Senior Associate receives a certificate, signed by SSI’s president, as a permanent record that he or she was one of the first people who gave critical support to the High Frontier. The names of the Senior Associates will also be permanently maintained by SSI to provide historians with the names of early High Frontier supporters.
Regular Membership
SSI Membership is open to individuals worldwide. All members receive the Institute’s newsletter, which is published bimonthly and keeps all SSI members abreast of SSI research, an SSI membership card and decal.
Membership fee: Regular $25.00; Senior Citizen or Student $15.00; non-US addresses, please add $10.00.
For gifts of $50.00 or more, you will receive an SSI lapel pin.
With gifts of $100.00 or more, you will receive a copy of Dr. O’Neill’s book, The High Frontier.
Volunteer Program
As a nonprofit organization, SSI relies on the expertise of many volunteers worldwide to assist in the areas of research, education, presentations, development of visual arts, and technical writing.
If you are interested in the future in space, contact SSI by letter, phone, FAX, or E-mail:
Space Studies Institute
P.O. Box 82
Princeton, NJ 08542.
Phone: 609-xxx-xxxx
FAX: 609-xxx-xxxx
E-mail: xxxx@psilink.com
[[librarian note: This address is here, as it was in the original printed newsletter, for historical reasons. It is no longer the physical address of SSI. For contributions, please see this page]]
©space studies institute
NEXT: 1994 May-Jun (Lunar concrete, SPS Report, Space Agriculture)